33 混合效应模型
\[ \def\bm#1{{\boldsymbol #1}} \]
I think that the formula language does allow expressions with ‘/’ to represent nested factors but I can’t check right now as there is a fire in the building where my office is located. I prefer to simply write nested factors as
factor1 + factor1:factor2.— Douglas Bates 1
混合效应模型在心理学、生态学、计量经济学和空间统计学等领域应用十分广泛。线性混合效应模型有多个化身,比如生态学里的分层线性模型(Hierarchical linear Model,简称 HLM),心理学的多水平线性模型(Multilevel Linear Model)。模型名称的多样性正说明它应用的广泛性! 混合效应模型内容非常多,非常复杂,因此,本章仅对常见的四种类型提供入门级的实战内容。从频率派和贝叶斯派两个角度介绍模型结构及说明、R 代码或 Stan 代码实现及输出结果解释。
除了 R 语言社区提供的开源扩展包,商业的软件有 Mplus 、ASReml 和 SAS 等,而开源的软件 OpenBUGS 、 JAGS 和 Stan 等。混合效应模型的种类非常多,一部分可以在一些流行的 R 包能力范围内解决,其余可以放在更加灵活、扩展性强的框架 Stan 内解决。因此,本章同时介绍 Stan 框架和一些 R 包。
本章用到 4 个数据集,其中 sleepstudy 和 cbpp 均来自 lme4 包 (Bates 等 2015),分别用于介绍线性混合效应模型和广义线性混合效应模型,Loblolly 来自 datasets 包,用于介绍非线性混合效应模型,最后,朗格拉普岛核辐射数据数据集用于介绍广义可加混合效应模型。
在介绍理论的同时给出 R 语言或 S 语言实现的几本参考书籍。
- 《Mixed-Effects Models in S and S-PLUS》(Pinheiro 和 Bates 2000)
- 《Mixed Models: Theory and Applications with R》(Demidenko 2013)
- 《Linear Mixed-Effects Models Using R: A Step-by-Step Approach》(Gałecki 和 Burzykowski 2013)
- 《Linear and Generalized Linear Mixed Models and Their Applications》(Jiang 和 Nguyen 2021)
33.1 线性混合效应模型
I think what we are seeking is the marginal variance-covariance matrix of the parameter estimators (marginal with respect to the random effects random variable, B), which would have the form of the inverse of the crossproduct of a \((q+p)\) by \(p\) matrix composed of the vertical concatenation of \(-L^{-1}RZXRX^{-1}\) and \(RX^{-1}\). (Note: You do not want to calculate the first term by inverting \(L\), use
solve(L, RZX, system = "L")
[…] don’t even think about using
solve(L)don’t!, don’t!, don’t!
have I made myself clear?
don’t do that (and we all know that someone will do exactly that for a very large \(L\) and then send out messages about “R is SOOOOO SLOOOOW!!!!” :-) )
— Douglas Bates 2
- 一般的模型结构和假设
- 一般的模型表达公式
-
nlme 包的函数
lme() - 公式语法和示例模型表示
线性混合效应模型(Linear Mixed Models or Linear Mixed-Effects Models,简称 LME 或 LMM),介绍模型的基础理论,包括一般形式,矩阵表示,参数估计,假设检验,模型诊断,模型评估。参数方法主要是极大似然估计和限制极大似然估计。一般形式如下:
\[ \bm{y} = X\bm{\beta} + Z\bm{u} + \bm{\epsilon} \]
其中,\(\bm{y}\) 是一个向量,代表响应变量,\(X\) 代表固定效应对应的设计矩阵,\(\bm{\beta}\) 是一个参数向量,代表固定效应对应的回归系数,\(Z\) 代表随机效应对应的设计矩阵,\(\bm{u}\) 是一个参数向量,代表随机效应对应的回归系数,\(\bm{\epsilon}\) 表示残差向量。
一般假定随机向量 \(\bm{u}\) 服从多元正态分布,这是无条件分布,随机向量 \(\bm{y}|\bm{u}\) 服从多元正态分布,这是条件分布。
\[ \begin{aligned} \bm{u} &\sim \mathcal{N}(0,\Sigma) \\ \bm{y}|\bm{u} &\sim \mathcal{N}(X\bm{\beta} + Z\bm{u},\sigma^2W) \end{aligned} \]
其中,方差协方差矩阵 \(\Sigma\) 必须是半正定的,\(W\) 是一个对角矩阵。
nlme 和 lme4 等 R 包共用一套表示随机效应的公式语法,如下表所示。
| 公式 | 含义 |
|---|---|
(1|group) |
随机组截距 |
(x|group) = (1+x|group)
|
变量 x 的随机组斜率和相关截距 |
(0+x|group) = (-1+x|group)
|
变量 x 的随机组斜率,无变化的截距 |
(1|group) + (0+x|group) |
不相关的随机截距,组内随机斜率 |
(1|site/block) = (1|site)+(1|site:block)
|
intercept varying among sites and among blocks within sites (nested random effects) |
site+(1|site:block) |
fixed effect of sites plus random variation in intercept among blocks within sites |
(x|site/block) = (x|site)+(x|site:block) = (1 + x|site)+(1+x|site:block)
|
slope and intercept varying among sites and among blocks within sites |
(x1|site)+(x2|block) |
two different effects, varying at different levels |
x*site+(x|site:block) |
fixed effect variation of slope and intercept varying among sites and random variation of slope and intercept among blocks within sites |
(1|group1)+(1|group2) |
intercept varying among crossed random effects (e.g. site, year) |
sleepstudy 数据集来自 lme4 包,是一个睡眠研究项目的实验数据。实验对象都是有失眠情况的人,有的人有严重的失眠问题(一天只有 3 个小时的睡眠时间)。进入实验后的前10 天的情况,记录平均反应时间、睡眠不足的天数。
#> 'data.frame': 180 obs. of 3 variables:
#> $ Reaction: num 250 259 251 321 357 ...
#> $ Days : num 0 1 2 3 4 5 6 7 8 9 ...
#> $ Subject : Factor w/ 18 levels "308","309","310",..: 1 1 1 1 1 1 1 1 1 1 ...Reaction 表示平均反应时间(毫秒),数值型,Days 表示进入实验后的第几天,数值型,Subject 表示参与实验的个体编号,因子型。
#> Subject
#> Days 308 309 310 330 331 332 333 334 335 337 349 350 351 352 369 370 371 372
#> 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 7 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 8 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> 9 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1每个个体每天产生一条数据,下 @fig-sleepstudy-line 中每条折线代表一个个体。
library(ggplot2)
ggplot(data = sleepstudy, aes(x = Days, y = Reaction, group = Subject)) +
geom_line() +
scale_x_continuous(n.breaks = 6) +
theme_bw() +
labs(x = "睡眠不足的天数", y = "平均反应时间")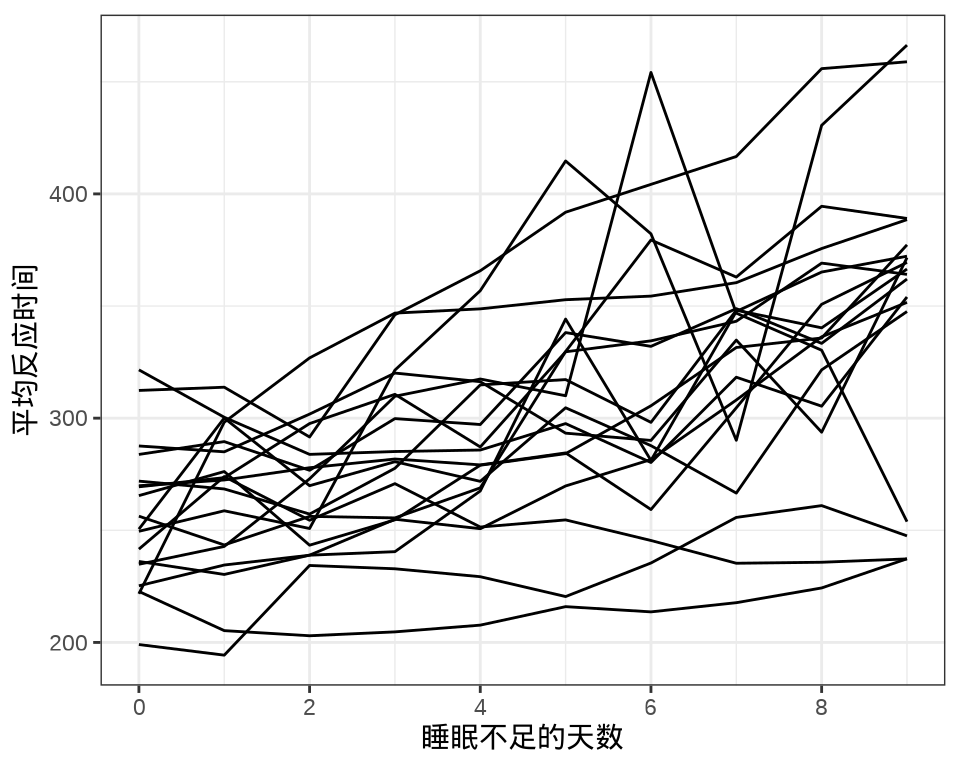
对于连续重复测量的数据(continuous repeated measurement outcomes),也叫纵向数据(longitudinal data),针对不同个体 Subject,相比于上图,下面绘制反应时间 Reaction 随睡眠时间 Days 的变化趋势更合适。图中趋势线是简单线性回归的结果,分面展示不同个体Subject 之间对比。
ggplot(data = sleepstudy, aes(x = Days, y = Reaction)) +
geom_point() +
geom_smooth(formula = "y ~ x", method = "lm", se = FALSE) +
scale_x_continuous(n.breaks = 6) +
theme_bw() +
facet_wrap(facets = ~Subject, labeller = "label_both", ncol = 6) +
labs(x = "睡眠不足的天数", y = "平均反应时间")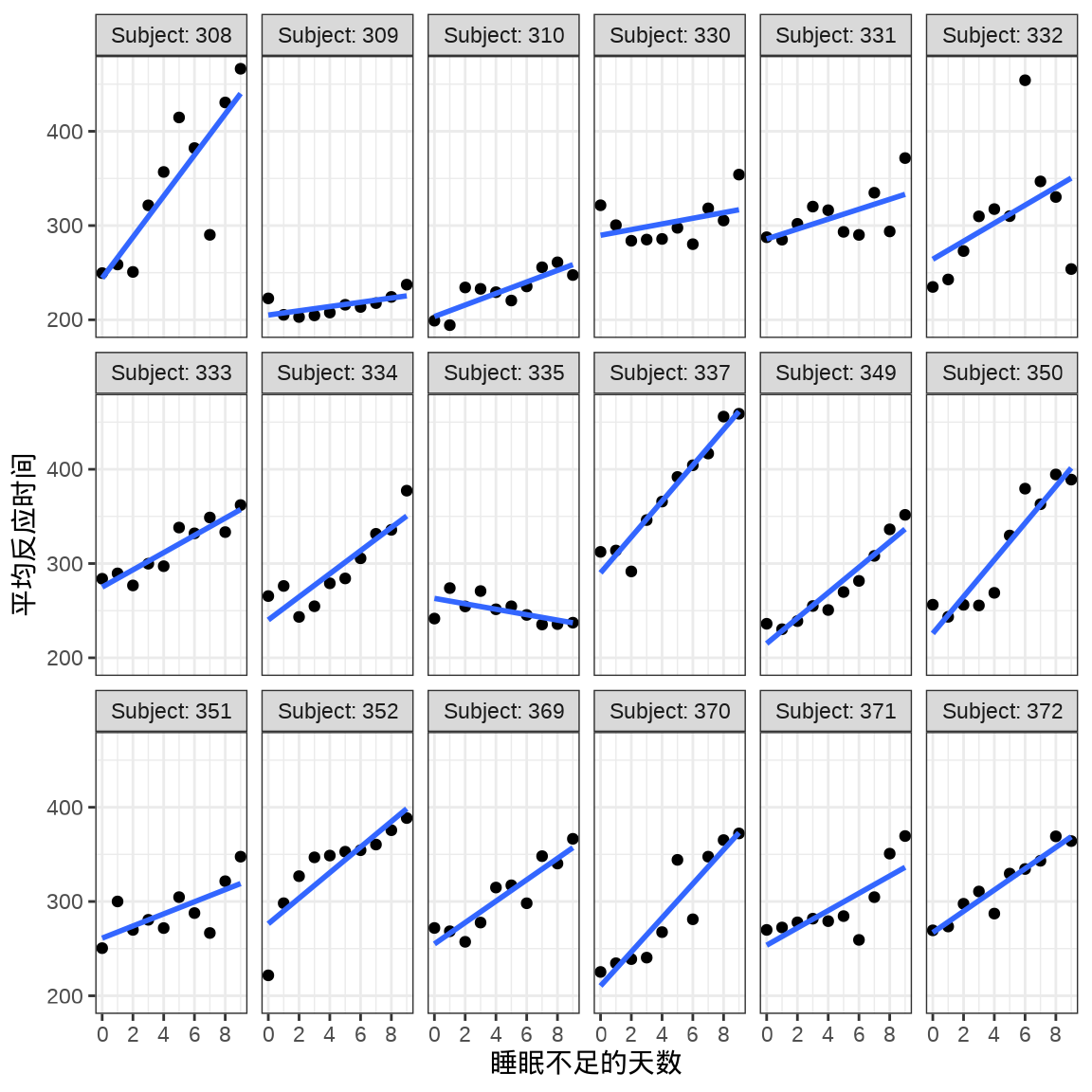
考虑两水平的混合效应模型,其中随机截距 \(\beta_{0j}\) 和随机斜率 \(\beta_{1j}\),指标 \(j\) 表示分组的编号,也叫变截距和变斜率模型
\[ \begin{aligned} \mathrm{Reaction}_{ij} &= \beta_{0j} + \beta_{1j} \cdot \mathrm{Days}_{ij} + \epsilon_{ij} \\ \beta_{0j} &= \gamma_{00} + U_{0j} \\ \beta_{1j} &= \gamma_{10} + U_{1j} \\ \begin{pmatrix} U_{0j} \\ U_{1j} \end{pmatrix} &\sim \mathcal{N} \begin{bmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \begin{pmatrix} \tau^2_{00} & \tau_{01} \\ \tau_{01} & \tau^2_{10} \end{pmatrix} \end{bmatrix} \\ \epsilon_{ij} &\sim \mathcal{N}(0, \sigma^2) \\ i = 0,1,\cdots,9 &\quad j = 308,309,\cdots, 372. \end{aligned} \]
下面用 nlme 包 (Pinheiro 和 Bates 2000) 拟合模型。
library(nlme)
fm1 <- lme(Reaction ~ Days, random = ~ Days | Subject, data = sleepstudy)
summary(fm1)#> Linear mixed-effects model fit by REML
#> Data: sleepstudy
#> AIC BIC logLik
#> 1755.628 1774.719 -871.8141
#>
#> Random effects:
#> Formula: ~Days | Subject
#> Structure: General positive-definite, Log-Cholesky parametrization
#> StdDev Corr
#> (Intercept) 24.740241 (Intr)
#> Days 5.922103 0.066
#> Residual 25.591843
#>
#> Fixed effects: Reaction ~ Days
#> Value Std.Error DF t-value p-value
#> (Intercept) 251.40510 6.824516 161 36.83853 0
#> Days 10.46729 1.545783 161 6.77151 0
#> Correlation:
#> (Intr)
#> Days -0.138
#>
#> Standardized Within-Group Residuals:
#> Min Q1 Med Q3 Max
#> -3.95355735 -0.46339976 0.02311783 0.46339621 5.17925089
#>
#> Number of Observations: 180
#> Number of Groups: 18随机效应(Random effects)部分:
#> (Intercept) Days
#> 308 2.258754 9.1989366
#> 309 -40.398490 -8.6197167
#> 310 -38.960098 -5.4489048
#> 330 23.690228 -4.8142826
#> 331 22.259981 -3.0698548
#> 332 9.039458 -0.2721585固定效应(Fixed effects)部分:
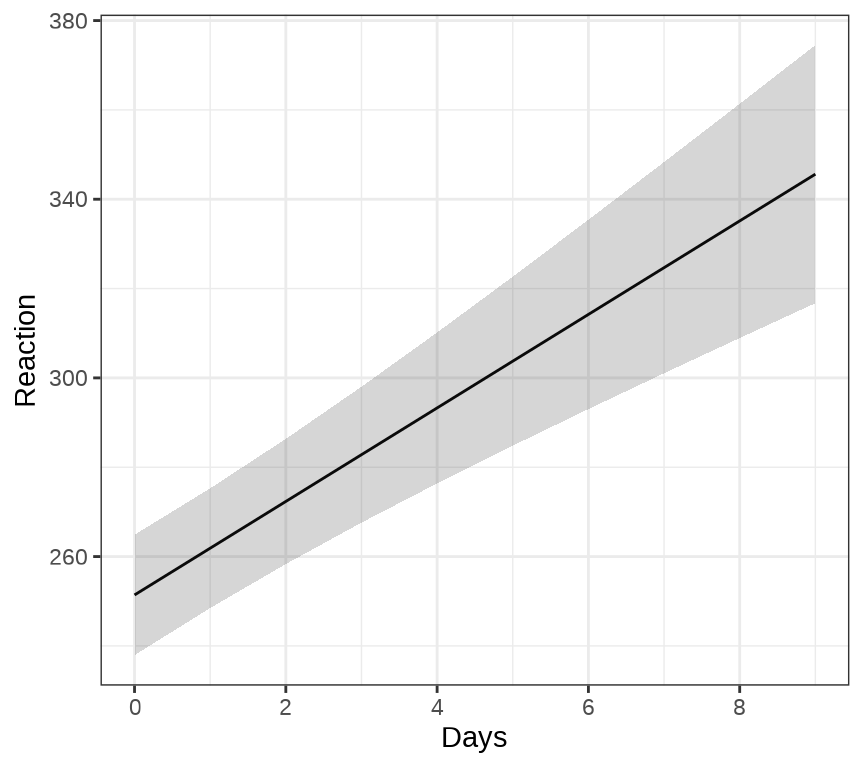
ggeffects 包的函数 ggpredict() 和 ggeffect() 可以用来绘制混合效应模型的边际效应( Marginal Effects),ggPMX 包 可以用来绘制混合效应模型的诊断图。下 图 33.3 展示关于变量 Days 的边际效应图。
33.2 广义线性混合效应模型
当响应变量分布不再是高斯分布,线性混合效应模型就扩展到广义线性混合效应模型。有一些 R 包可以拟合此类模型,MASS 包的函数 glmmPQL() ,lme4 包的函数 glmer() ,GLMMadaptive 包的函数 mixed_model() ,brms 包的函数 brm() 等。
| 响应变量分布 | MASS | lme4 | GLMMadaptive | brms |
|---|---|---|---|---|
| 伯努利分布 | 支持 | 支持 | 支持 | 支持 |
| 二项分布 | 支持 | 支持 | 支持 | 支持 |
| 泊松分布 | 支持 | 支持 | 支持 | 支持 |
| 负二项分布 | 不支持 | 支持 | 支持 | 支持 |
| 伽马分布 | 支持 | 支持 | 支持 | 支持 |
函数 glmmPQL() 支持的分布族见函数 glm() 的参数 family ,lme4 包的函数 glmer.nb() 和 GLMMadaptive 包的函数 negative.binomial() 都可用于拟合响应变量服从负二项分布的情况。除了这些常规的分布,GLMMadaptive 和 brms 包还支持许多常见的分布,比如零膨胀的泊松分布、二项分布等,还可以自定义分布。
- 伯努利分布
family = binomial(link = "logit") - 二项分布
family = binomial(link = "logit") - 泊松分布
family = poisson(link = "log") - 负二项分布
lme4::glmer.nb()或GLMMadaptive::negative.binomial() - 伽马分布
family = Gamma(link = "inverse")
GLMMadaptive 包 (Rizopoulos 2023) 的主要函数 mixed_model() 是用来拟合广义线性混合效应模型的。下面以牛传染性胸膜肺炎(Contagious bovine pleuropneumonia,简称 CBPP)数据 cbpp 介绍函数 mixed_model() 的用法,该数据集来自 lme4 包。
#> 'data.frame': 56 obs. of 4 variables:
#> $ herd : Factor w/ 15 levels "1","2","3","4",..: 1 1 1 1 2 2 2 3 3 3 ...
#> $ incidence: num 2 3 4 0 3 1 1 8 2 0 ...
#> $ size : num 14 12 9 5 22 18 21 22 16 16 ...
#> $ period : Factor w/ 4 levels "1","2","3","4": 1 2 3 4 1 2 3 1 2 3 ...herd 牛群编号,period 时间段,incidence 感染的数量,size 牛群大小。疾病在种群内扩散
ggplot(data = cbpp, aes(x = herd, y = period)) +
geom_tile(aes(fill = incidence / size)) +
scale_fill_viridis_c(label = scales::percent_format(),
option = "C", name = "") +
theme_minimal()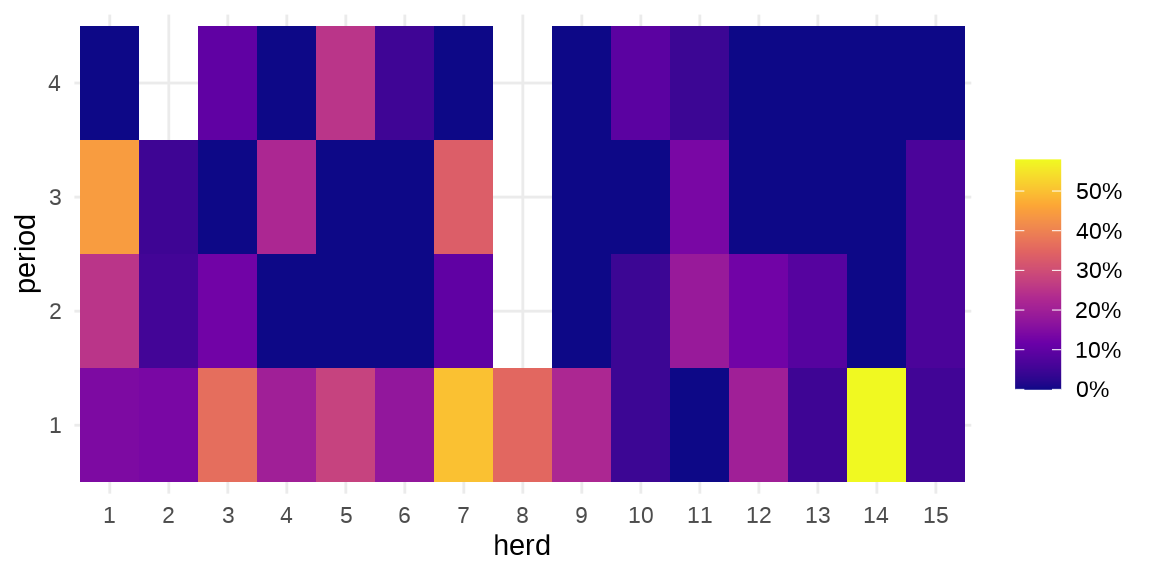
library(GLMMadaptive)
fgm1 <- mixed_model(
fixed = cbind(incidence, size - incidence) ~ period,
random = ~ 1 | herd, data = cbpp, family = binomial(link = "logit")
)
summary(fgm1)#>
#> Call:
#> mixed_model(fixed = cbind(incidence, size - incidence) ~ period,
#> random = ~1 | herd, data = cbpp, family = binomial(link = "logit"))
#>
#> Data Descriptives:
#> Number of Observations: 56
#> Number of Groups: 15
#>
#> Model:
#> family: binomial
#> link: logit
#>
#> Fit statistics:
#> log.Lik AIC BIC
#> -91.98337 193.9667 197.507
#>
#> Random effects covariance matrix:
#> StdDev
#> (Intercept) 0.6475934
#>
#> Fixed effects:
#> Estimate Std.Err z-value p-value
#> (Intercept) -1.3995 0.2335 -5.9923 < 1e-04
#> period2 -0.9914 0.3068 -3.2316 0.00123091
#> period3 -1.1278 0.3268 -3.4513 0.00055793
#> period4 -1.5795 0.4276 -3.6937 0.00022101
#>
#> Integration:
#> method: adaptive Gauss-Hermite quadrature rule
#> quadrature points: 11
#>
#> Optimization:
#> method: EM
#> converged: TRUE33.3 非线性混合效应模型
Loblolly 数据集来自 R 内置的 datasets 包
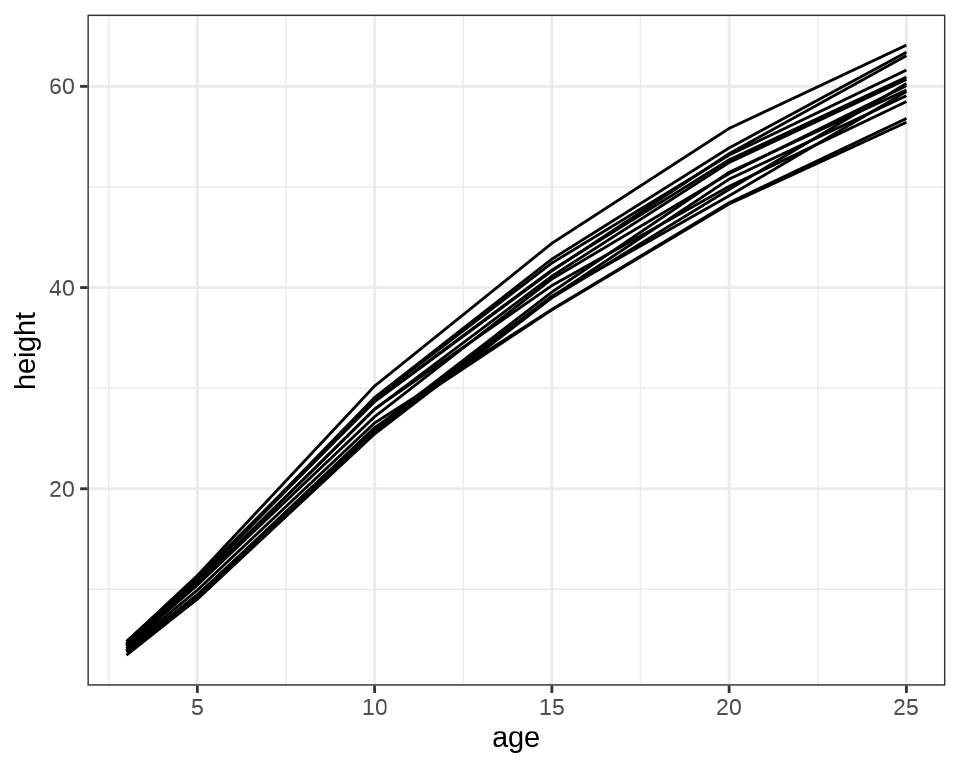
非线性回归
nfm1 <- nls(height ~ SSasymp(age, Asym, R0, lrc),
data = Loblolly, subset = Seed == 329)
summary(nfm1)#>
#> Formula: height ~ SSasymp(age, Asym, R0, lrc)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Asym 94.1282 8.4030 11.202 0.001525 **
#> R0 -8.2508 1.2261 -6.729 0.006700 **
#> lrc -3.2176 0.1386 -23.218 0.000175 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.7493 on 3 degrees of freedom
#>
#> Number of iterations to convergence: 0
#> Achieved convergence tolerance: 4.148e-07非线性函数 SSasymp() 的内容如下
\[ \mathrm{Asym}+(\mathrm{R0}-\mathrm{Asym})\times\exp\big(-\exp(\mathrm{lrc})\times\mathrm{input}\big) \]
其中,\(\mathrm{Asym}\) 、\(\mathrm{R0}\) 、\(\mathrm{lrc}\) 是参数,\(\mathrm{input}\) 是输入值。
示例来自 nlme 包的函数 nlme() 帮助文档
nfm2 <- nlme(height ~ SSasymp(age, Asym, R0, lrc),
data = Loblolly,
fixed = Asym + R0 + lrc ~ 1,
random = Asym ~ 1,
start = c(Asym = 103, R0 = -8.5, lrc = -3.3)
)
summary(nfm2)#> Nonlinear mixed-effects model fit by maximum likelihood
#> Model: height ~ SSasymp(age, Asym, R0, lrc)
#> Data: Loblolly
#> AIC BIC logLik
#> 239.4856 251.6397 -114.7428
#>
#> Random effects:
#> Formula: Asym ~ 1 | Seed
#> Asym Residual
#> StdDev: 3.650642 0.7188625
#>
#> Fixed effects: Asym + R0 + lrc ~ 1
#> Value Std.Error DF t-value p-value
#> Asym 101.44960 2.4616951 68 41.21128 0
#> R0 -8.62733 0.3179505 68 -27.13420 0
#> lrc -3.23375 0.0342702 68 -94.36052 0
#> Correlation:
#> Asym R0
#> R0 0.704
#> lrc -0.908 -0.827
#>
#> Standardized Within-Group Residuals:
#> Min Q1 Med Q3 Max
#> -2.23601930 -0.62380854 0.05917466 0.65727206 1.95794425
#>
#> Number of Observations: 84
#> Number of Groups: 14#> Nonlinear mixed-effects model fit by maximum likelihood
#> Model: height ~ SSasymp(age, Asym, R0, lrc)
#> Data: Loblolly
#> AIC BIC logLik
#> 238.9662 253.5511 -113.4831
#>
#> Random effects:
#> Formula: list(Asym ~ 1, lrc ~ 1)
#> Level: Seed
#> Structure: Diagonal
#> Asym lrc Residual
#> StdDev: 2.806185 0.03449969 0.6920003
#>
#> Fixed effects: Asym + R0 + lrc ~ 1
#> Value Std.Error DF t-value p-value
#> Asym 101.85205 2.3239828 68 43.82651 0
#> R0 -8.59039 0.3058441 68 -28.08747 0
#> lrc -3.24011 0.0345017 68 -93.91167 0
#> Correlation:
#> Asym R0
#> R0 0.727
#> lrc -0.902 -0.796
#>
#> Standardized Within-Group Residuals:
#> Min Q1 Med Q3 Max
#> -2.06072906 -0.69785679 0.08721706 0.73687722 1.79015782
#>
#> Number of Observations: 84
#> Number of Groups: 14代码
library(brms)
lob_prior <- c(
set_prior("normal(101, 0.1)", nlpar = "Asym", lb = 100, ub = 102),
set_prior("normal(-8, 1)", nlpar = "R0", lb = -10),
set_prior("normal(-3, 3)", nlpar = "lrc", lb = -9),
set_prior("normal(3, 0.2)", class = "sigma")
)
lob_formula <- bf(
height ~ Asym + (R0 - Asym) * exp( - exp(lrc) * age),
# Nonlinear variables
# Fixed effects: Asym R0 lrc
R0 + lrc ~ 1,
# Nonlinear variables
# Random effects: Seed
Asym ~ 1 + (1 | Seed),
# Nonlinear fit
nl = TRUE
)
lob_bayes_fit <- brm(
lob_formula, family = gaussian(), data = Loblolly, prior = lob_prior
)33.4 总结
本章介绍函数 MASS::glmmPQL()、 nlme::lme()、lme4::lmer() 和 brms::brm() 的用法,以及它们求解线性混合效应模型的区别和联系。在贝叶斯估计方法中,brms 包和 INLA 包都支持非常丰富的模型种类,前者是贝叶斯精确推断,后者是贝叶斯近似推断,brms 基于概率编程语言 Stan 框架打包了许多模型的 Stan 实现,INLA 基于求解随机偏微分方程的有限元方法和拉普拉斯近似技巧,将各类常见统计模型统一起来,计算速度快,计算结果准确。
- 函数
nlme::lme()极大似然估计和限制极大似然估计 - 函数
MASS::glmmPQL()惩罚拟似然估计,MASS 是依赖 nlme 包, nlme 不支持模型中添加漂移项,所以函数glmmPQL()也不支持添加漂移项。 - 函数
lme4::lmer()拉普拉斯近似。关于随机效应的高维积分 - 函数
brms::brm()汉密尔顿蒙特卡罗抽样。HMC 方法结合自适应步长的采样器 NUTS 来抽样。 - 函数
INLA::inla()集成嵌套拉普拉斯近似。
| 模型 | nlme | MASS | lme4 | GLMMadaptive | brms |
|---|---|---|---|---|---|
| 线性混合效应模型 | lme() |
glmmPQL() |
lmer() |
不支持 | brm() |
| 广义线性混合效应模型 | 不支持 | glmmPQL() |
glmer() |
mixed_model() |
brm() |
| 非线性混合效应模型 | nlme() |
不支持 | nlmer() |
不支持 | brm() |
通过对频率派和贝叶斯派方法的比较,发现一些有意思的结果。与 Stan 不同,INLA 包做近似贝叶斯推断,计算效率很高。
INLA 软件能处理上千个高斯随机效应,但最多只能处理 15 个超参数,因为 INLA 使用 CCD 处理超参数。如果使用 MCMC 处理超参数,就有可能处理更多的超参数,Daniel Simpson 等把 Laplace approximation 带入 Stan,这样就可以处理上千个超参数。 更多理论内容见 2009 年 INLA 诞生的论文和《Advanced Spatial Modeling with Stochastic Partial Differential Equations Using R and INLA》中第一章的估计方法 CCD。
33.5 习题
基于奥克兰火山地形数据集 volcano ,随机拆分成训练数据和测试数据,训练数据可以看作采样点的观测数据,建立高斯过程回归模型,比较测试数据与未采样的位置上的预测数据,在计算速度、准确度、易用性等方面总结 Stan 和 INLA 的特点。
-
基于
PlantGrowth数据集,比较将group变量视为随机变量与随机效应的异同? -
从频率派和贝叶斯派角度分别比较多个 R 包对线性混合效应模型的拟合效果。提示:函数
MASS::glmmPQL()、函数lme4::lmer(),以及函数blme::blmer()和brms::brm()。代码
# 加载数据集 data(sleepstudy, package = "lme4") fit_lmm_mass <- MASS::glmmPQL(Reaction ~ Days, random = ~ Days | Subject, verbose = FALSE, data = sleepstudy, family = gaussian ) summary(fit_lmm_mass) coef(summary(fit_lmm_mass)) fit_lmm_lme4 <- lme4::lmer(Reaction ~ Days + (Days | Subject), data = sleepstudy) summary(fit_lmm_lme4) coef(summary(fit_lmm_lme4)) fit_lmm_blme <- blme::blmer( Reaction ~ Days + (Days | Subject), data = sleepstudy, control = lme4::lmerControl(check.conv.grad = "ignore"), cov.prior = gamma) summary(fit_lmm_blme) coef(summary(fit_lmm_blme)) fit_lmm_brms <- brms::brm(Reaction ~ Days + (Days | Subject), data = sleepstudy, refresh = 0 ) summary(fit_lmm_brms) -
从频率派和贝叶斯派角度分别比较多个 R 包对广义线性混合效应模型的拟合效果。提示:函数
MASS::glmmPQL()、函数lme4::glmer()和函数glmmTMB::glmmTMB(),以及函数blme::bglmer()和函数brms::brm()。代码
# 加载数据集 data(cbpp, package = "lme4") fit_glmm_mass <- MASS::glmmPQL( cbind(incidence, size - incidence) ~ period , random = ~ 1 | herd, verbose = FALSE, data = cbpp, family = binomial("logit") ) summary(fit_glmm_mass) coef(summary(fit_glmm_mass)) fit_glmm_lme4 <- lme4::glmer( cbind(incidence, size - incidence) ~ period + (1 | herd), family = binomial("logit"), data = cbpp ) summary(fit_glmm_lme4) fit_glmm_glmmtmb <- glmmTMB::glmmTMB( cbind(incidence, size - incidence) ~ period + (1 | herd), data = cbpp, family = binomial, REML = TRUE ) # REML 估计 summary(fit_glmm_glmmtmb) fit_glmm_blme <- blme::bglmer( cbind(incidence, size - incidence) ~ period + (1 | herd), family = binomial("logit"), data = cbpp ) summary(fit_glmm_blme) fit_glmm_brms <- brms::brm( incidence | trials(size) ~ period + (1 | herd), family = binomial("logit"), data = cbpp ) summary(fit_glmm_brms)或使用 mgcv 包,可以得到近似的结果。随机效应部分可以看作可加的惩罚项
library(mgcv) fgm3 <- gam( cbind(incidence, size - incidence) ~ period + s(herd, bs = "re"), data = cbpp, family = binomial(link = "logit"), method = "REML" ) summary(fgm3)#> #> Family: binomial #> Link function: logit #> #> Formula: #> cbind(incidence, size - incidence) ~ period + s(herd, bs = "re") #> #> Parametric coefficients: #> Estimate Std. Error z value Pr(>|z|) #> (Intercept) -1.3670 0.2358 -5.799 6.69e-09 *** #> period2 -0.9693 0.3040 -3.189 0.001428 ** #> period3 -1.1045 0.3241 -3.407 0.000656 *** #> period4 -1.5519 0.4251 -3.651 0.000261 *** #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> #> Approximate significance of smooth terms: #> edf Ref.df Chi.sq p-value #> s(herd) 9.66 14 32.03 3.21e-05 *** #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> #> R-sq.(adj) = 0.515 Deviance explained = 53% #> -REML = 93.199 Scale est. = 1 n = 56下面给出随机效应的标准差的估计及其上下限,和前面 GLMMadaptive 包和 lme4 包给出的结果也是接近的。
-
从广义线性混合效应模型生成模拟数据,用至少 6 个不同的 R 包估计模型参数,比较和归纳不同估计方法和实现算法的效果。举例:带漂移项的泊松型广义线性混合效应模型。\(y_{ij}\) 表示响应变量,\(\bm{u}\) 表示随机效应,\(o_{ij}\) 表示漂移项。
\[ \begin{aligned} y_{ij}|\bm{u} &\sim \mathrm{Poisson}(o_{ij}\lambda_{ij}) \\ \log(\lambda_{ij}) &= \beta_{ij}x_{ij} + u_{j} \\ u_j &\sim \mathcal{N}(0, \sigma^2) \\ i = 1,2,\ldots, n &\quad j = 1,2,\ldots,q \end{aligned} \]
代码
set.seed(2023) Ngroups <- 25 NperGroup <- 100 # 样本量 N <- Ngroups * NperGroup # 截距和两个协变量的系数 beta <- c(0.5, 0.3, 0.2) # 两个协变量 X <- MASS::mvrnorm(N, mu = rep(0, 2), Sigma = matrix(c(1, 0.8, 0.8, 1), 2)) # 漂移项 o <- rep(c(2, 4), each = N / 2) # 分 25 个组 每个组 100 个观察值 g <- factor(rep(1:Ngroups, each = NperGroup)) u <- rnorm(Ngroups, sd = .5) # 随机效应的标准差 0.5 # 泊松分布的期望 lambda <- o * exp(cbind(1, X) %*% beta + u[g]) # 响应变量的值 y <- rpois(N, lambda = lambda) # 模拟的数据集 sim_data <- data.frame(y, X, o, g) colnames(sim_data) <- c("y", "x1", "x2", "o", "g") # 模型拟合 library(lme4) fit_sim_poisson_glmer <- glmer(y ~ x1 + x2 + (1 | g), data = sim_data, offset = log(o), family = poisson(link = "log") ) # 模型输出 summary(fit_sim_poisson_glmer) # 对随机效应 adaptive Gauss-Hermite quadrature 积分 library(GLMMadaptive) fit_sim_poisson_adaptive <- mixed_model( fixed = y ~ x1 + x2 + offset(log(o)), random = ~ 1 | g, data = sim_data, family = poisson(link = "log") ) summary(fit_sim_poisson_adaptive) # 如何设置先验分布 fit_sim_poisson_brm <- brms::brm( y ~ x1 + x2 + (1 | g) + offset(log(o)), data = sim_data, family = poisson(link = "log"), # silent = 2, # 关闭消息 refresh = 0, # 不显示迭代进度 seed = 20232023, backend = "cmdstanr" # 选择后端 rstan 或 cmdstanr ) # 拟合结果 summary(fit_sim_poisson_brm) # 发散很多 plot(fit_sim_poisson_brm) # 模型诊断指标 brms::WAIC(fit_sim_poisson_brm) brms::pp_check(fit_sim_poisson_brm) # gee GLMMadaptive glmmML geepack 和 lme4 的模型输出结果是接近的 # blme 基于 lme4 的贝叶斯估计 library(blme) fit_sim_poisson_bglmer <- bglmer( formula = y ~ x1 + x2 + (1 | g), data = sim_data, offset = log(o), family = poisson(link = "log") ) summary(fit_sim_poisson_bglmer) # MCMCglmm 包 贝叶斯估计 fit_sim_poisson_mcmcglmm <- MCMCglmm::MCMCglmm( fixed = y ~ x1 + x2 + offset(log(o)), random = ~g, family = "poisson", data = sim_data, verbose = FALSE ) summary(fit_sim_poisson_mcmcglmm) ## hglm 包 Hierarchical Generalized Linear Models # extended quasi likelihood (EQL) method fit_sim_poisson_hglm <- hglm::hglm( fixed = y ~ x1 + x2, random = ~ 1 | g, family = poisson(link = "log"), offset = log(o), data = sim_data ) summary(fit_sim_poisson_hglm) # 广义估计方程 library(gee) fit_sim_poisson_gee <- gee(y ~ x1 + x2 + offset(log(o)), id = g, data = sim_data, family = poisson(link = "log"), corstr = "exchangeable" ) # 输出 fit_sim_poisson_gee # [glmmML](https://CRAN.R-project.org/package=glmmML) # Maximum Likelihood and numerical integration via Gauss-Hermite quadrature. library(glmmML) fit_sim_poisson_glmmml <- glmmML( formula = y ~ x1 + x2, family = poisson, data = sim_data, offset = log(o), cluster = g ) summary(fit_sim_poisson_glmmml) # Generalized Estimating Equation # [geepack](https://cran.r-project.org/package=geepack) GEE library(geepack) fit_sim_poisson_geepack <- geeglm( formula = y ~ x1 + x2, family = poisson(link = "log"), id = g, offset = log(o), data = sim_data, corstr = "exchangeable", scale.fix = FALSE ) summary(fit_sim_poisson_geepack) # [glmm](https://github.com/knudson1/glmm) # Monte Carlo Likelihood Approximation 近似对随机效应的积分 library(glmm) set.seed(2023) # 设置双核并行迭代 clust <- makeCluster(2) # doParallel # 对迭代时间没有给出预估,一旦执行,不知道什么时候会跑完 fit_sim_poisson_glmm <- glmm(y ~ x1 + x2 + offset(log(o)), random = list(~ 1 + g), # 随机效应 varcomps.names = "G", # 给随机效应取个名字 data = sim_data, family.glmm = poisson.glmm, # 泊松型 m = 10^4, debug = TRUE, cluster = clust ) stopCluster(clust) summary(fit_sim_poisson_glmm) -
基于 MASS 包的地形数据集 topo,建立高斯过程回归模型,比较贝叶斯预测与克里金插值预测的效果。
代码
data(topo, package = "MASS") set.seed(20232023) nchains <- 2 # 2 条迭代链 # 给每条链设置不同的参数初始值 inits_data_gaussian <- lapply(1:nchains, function(i) { list( beta = rnorm(1), sigma = runif(1), phi = runif(1), tau = runif(1) ) }) # 预测区域网格化 nx <- ny <- 27 topo_grid_df <- expand.grid( x = seq(from = 0, to = 6.5, length.out = nx), y = seq(from = 0, to = 6.5, length.out = ny) ) # 对数高斯模型 topo_gaussian_d <- list( N1 = nrow(topo), # 观测记录的条数 N2 = nrow(topo_grid_df), D = 2, # 2 维坐标 x1 = topo[, c("x", "y")], # N x 2 坐标矩阵 x2 = topo_grid_df[, c("x", "y")], y1 = topo[, "z"] # N 向量 ) library(cmdstanr) # 编码 mod_topo_gaussian <- cmdstan_model( stan_file = "code/gaussian_process_pred.stan", compile = TRUE, cpp_options = list(stan_threads = TRUE) ) # 高斯过程回归模型 fit_topo_gaussian <- mod_topo_gaussian$sample( data = topo_gaussian_d, # 观测数据 init = inits_data_gaussian, # 迭代初值 iter_warmup = 500, # 每条链预处理迭代次数 iter_sampling = 1000, # 每条链总迭代次数 chains = nchains, # 马尔科夫链的数目 parallel_chains = 2, # 指定 CPU 核心数,可以给每条链分配一个 threads_per_chain = 1, # 每条链设置一个线程 show_messages = FALSE, # 不显示迭代的中间过程 refresh = 0, # 不显示采样的进度 output_dir = "data-raw/", seed = 20232023 ) # 诊断 fit_topo_gaussian$diagnostic_summary() # 对数高斯模型 fit_topo_gaussian$summary( variables = c("lp__", "beta", "sigma", "phi", "tau"), .num_args = list(sigfig = 4, notation = "dec") ) # 未采样的位置的预测值 ypred <- fit_topo_gaussian$summary(variables = "ypred", "mean") # 预测值 topo_grid_df$ypred <- ypred$mean # 整理数据 library(sf) topo_grid_sf <- st_as_sf(topo_grid_df, coords = c("x", "y"), dim = "XY") library(stars) # 26x26 的网格 topo_grid_stars <- st_rasterize(topo_grid_sf, nx = 26, ny = 26) library(ggplot2) ggplot() + geom_stars(data = topo_grid_stars, aes(fill = ypred)) + scale_fill_viridis_c(option = "C") + theme_bw() -
用 brms 包实现贝叶斯高斯过程回归模型,考虑用样条近似高斯过程以加快计算。提示:brms 包的函数
gp()的参数 \(k\) 表示近似高斯过程 GP 所用的基函数的数目。截止写作时间,函数gp()的参数cov只能取指数二次核函数 exponentiated-quadratic kernel 。代码
# 高斯过程近似计算 bgamm2 <- brms::brm( z ~ gp(x, y, cov = "exp_quad", c = 5 / 4, k = 50), data = topo, chains = 2, seed = 20232023, warmup = 1000, iter = 2000, thin = 1, refresh = 0, control = list(adapt_delta = 0.99) ) # 输出结果 summary(bgamm2) # 条件效应 me3 <- brms::conditional_effects(bgamm1, ndraws = 200, spaghetti = TRUE) # 绘制图形 plot(me3, ask = FALSE, points = TRUE)